在我的上两篇文章中，介绍了物料存储的不同方法。这篇文章我们将继续看物料应该存放在什么位置。我们会探讨不同的选择，希望可以帮助你找到适合你的方式。关于存放位置的第一篇文会讨论固定位置存储，以及解释为什么这种方法不是优先选项。
目标
通常情况下，任何一种存储单元都有三个主要的关键指标。根据你的存储方法，有不同的权衡。这三个主要的指标是：
- 存取成本：物料进出仓库的存取成本。通常情况下，提取和存入的成本相近，只是提取的数量通常较少，但更频繁。存入大量的物料可能需要起重设备（如叉车、托盘升降机等），而提取则可以简单手动进行。对于滚轮式货架，存入和提取也可能在货架的不同端进行。当然，目标是降低成本。
- 增加存取的频率：存入和提取一个物料需要多少时间。或者说，每小时能拿到多少物料。这与成本有关，因为你可以通过增加员工或设备数量轻松地增加取货频率。这里的目标是在给定数量的人工或设备的情况下获得最多数量的物料。这里的主要因素是物料提取所需的行走距离。
- 空间利用率：你能如何有效地利用空间（即，你能把多少物料存入仓库）。100%的使用存储空间是不现实的，总是需要一些空位，以方便挪出所需的物料。给物料分配固定的位置，通常会使空间利用率降低。
固定位置存储
存储策略的主要选项之一是，是否需要使用固定位置来存储物料，即每一个存储空间分配给特定型号。
这种方式的优势是，在没有计算机的帮助下，更容易找到物料。由于每个型号物料的位置是固定的，可以很容易将物料布局画出来。货架上可以贴上物料型号的标签，员工们也可以很快地记住物料的位置，这种方式减少了寻找物料的时间。
反过来，它又会大大降低存储空间利用率。需要为每个型号分配足够的存储空间，以覆盖最大的存储需求。这意味着整个存储空间大部分时间都有空位，这些空位不能用于存储其他物料。总之，你所需要的存储空间要比随机存储方式多得多。
固定位置存储的计算实例
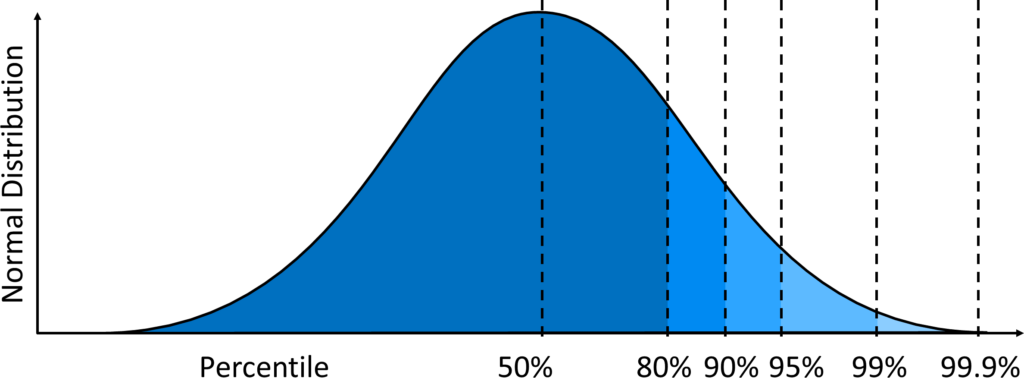
让我们继续深入地研究下这个问题。首先，假设你有一个物料，平均库存为μ = 10件。由于存储需求是波动的，为了简化数学计算，让我们假设这个库存符合正态分布，标准差σ为平均值的50%，即σ=5件。如果你正好只有10个零件的存储空间，那么几乎一半时间你无法继续存入物料，这种状态肯定会导致很多问题。
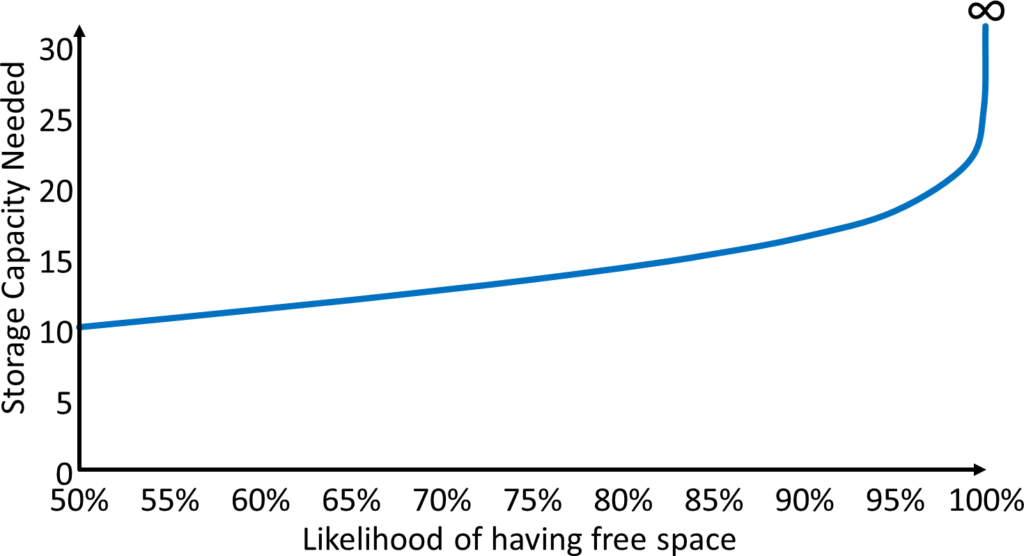
如果你想在80%的情况下能够存入物料（仍有20%的时间会有问题），需要增加0.84个标准差（也就是说，需要14个零件的空间）。想要覆盖的波动越多，需要的存储空间也就越大。这个关系不是线性的，对于更高的需求，所需的存储空间会急剧增加。如果想让任何情况下一直有空余存储空间可用，那么存储空间会是无限大。即使只覆盖99%的情况，存储空间也会增加一倍，需要22个。
现实情况会稍微好一点，你会遇到不同的存储需求的分布，不大会碰到”无限”的存储空间。就算遇到，你还有一些其它的应对措施，如多销售一些，少订购一些或者干脆租用更多的存储空间。但无论如何，你肯定需要比平均存储需求多一些存储空间，以覆盖波动。
我们再假设一个比较现实的情况，考虑存储可靠性为95%。通过计算，你需要为这个物料分配18个存储空间。如果你现在有1000种型号的物料，每种物料的平均存储需求均为10，标准差都为5，那么将需要18000个存储空间（18×1000）。
随机位置存储的计算实例
如果你没有为每个零件分配一个固定的位置，这看起来区别就大了。在这种情况下，一个物料对存储空间的过度需求可能会被另一个物料的低需求所抵消。我们还是以1000个物料为例，每个物料的平均值为10，标准差为5。所有型号物料的综合平均数仍然是1000*10=10,000个零件。但是，标准差σ的计算方式不同，如下图所示：
和
因此，σ=5的1000个零件的综合标准偏差不是1000×5=5000，而是只有158。
因此，我们的平均存储需求为10,000个零件，其标准偏差仅为158个零件。计算覆盖95%的情况所需的存储空间，只需要10,260个。这与固定存储位置所需的18,000个存储空间比少了很多。
下面是我们这个例子的具体图示。y轴显示你需要多少存储空间来覆盖一定比例的情况，x轴显示了我们有多少种不同型号的物料。需要的总平均存储量是10000个零件，波动的标准差是平均值的一半（如果改变平均值和标准差，仍可以得到一个非常相似的图形）。上面的水平线是针对固定位置存储的情况，如果你只有1个型号的物料，有10000件，还是有1000个型号的物料，每个型号各10件，这并不重要，对于我们想要覆盖情况，需要总库存的数量是一样的。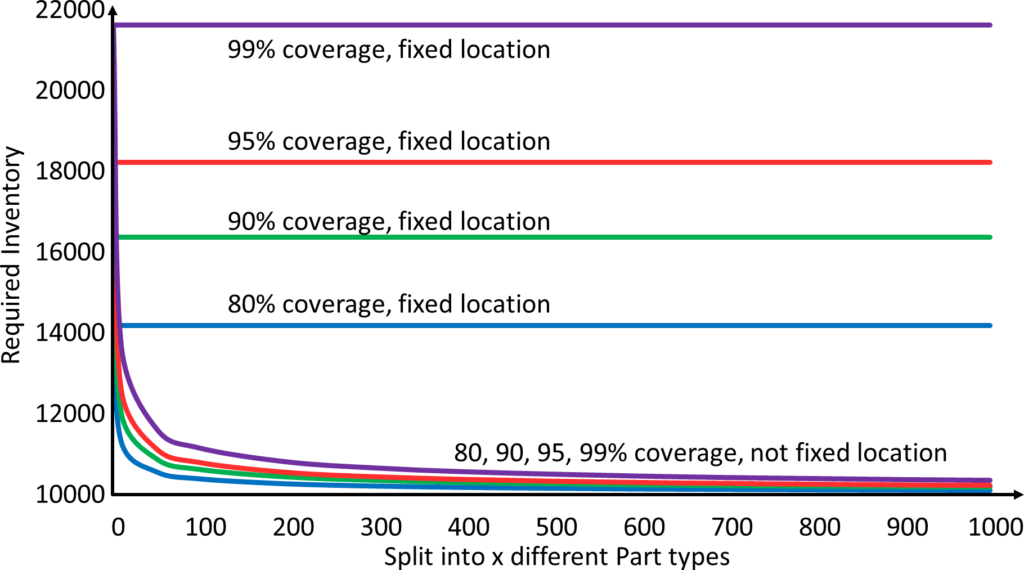 
然而，如果是随机位置存储，情况就不同了。在这种情况下，对于只有1种型号，这个型号有10000件的平均存储量，那么这和固定位置存储的情况相同。但是如果型号越多，那么我们需要的存储空间就越少，也越接近于10000这个平均值。
理论模型的注意事项
看起来，如果不使用固定位置存储，你几乎可以节省大部分多余空间来弥补库存的波动。这听起好像有点问题。
嗯，这里面的确有些问题。首先，这是一个简单的数学模型，我们使用了很多假设。在实际情况，波动可能不是正态分布，正态分布的边界是±∞，而且实际不可能库存为负值。
其次，我们假设这些变量是相互独立的。然而，在现实中，一个物料的库存水平经常依赖于另一个物料。例如，如果是旺季，会比淡季有更多的东西。因此在旺季的随机位置存储的情况下，存储空间需求可能比理论模型高得多。当然，它仍然会比有固定位置存储的情况低得多。低多少？这取决于很多因素，也很难计算，试一下就知道了！
何时使用固定位置存储
那么，什么时候应该使用固定存储位置？其实反过来问，什么时候不使用固定位置存储？更容易回答。如果存储空间很紧张，而且存储空间几乎耗尽了，那么应该避免为零件分配固定位置。同样，如果是按订单生产方式，并且库存中经常有许多定制的零件，那么给这个“每年生产一次”的零件分配一个固定的位置也是没有意义的。
反过来，如果你有足够的存储空间，那么……我还是会谨慎使用固定位置存储。如果你有足够的空间，但物料数量较多，而且追踪零件的系统很复杂（即，如果只是手动记录零件的位置，那么任何改变都需要花时间，还有可能出错），那么使用固定位置可能是一个不错的选择。你越少改变存储位置，管理起来就越容易，在Excel中管理存储位置，也同样适用。
总的来说，固定位置存储的不是流行方法。不过，也会在一些混合系统中会使用。我将在下面的文章中讨论其他系统和混合系统。在那之前，请继续关注，走出去，组织你的行业！
系列文章
Translated by Xie Xuan