 这篇文章描述了识别生产系统中瓶颈的第二种精确方法,基于一个过程等待或活跃的精确时间。该方法非常准确,不仅能给出不同工序成为(瞬时)瓶颈的可能性,而且还能估计出如果瓶颈得到改善,整个系统产能能提升多少。还可以观察这些瓶颈随着时间的推移而发生的变化。该方法是我在日本丰田中央研发实验室工作期间开发的。请看下面关于瓶颈问题的系列文章的完整列表 。
这篇文章描述了识别生产系统中瓶颈的第二种精确方法,基于一个过程等待或活跃的精确时间。该方法非常准确,不仅能给出不同工序成为(瞬时)瓶颈的可能性,而且还能估计出如果瓶颈得到改善,整个系统产能能提升多少。还可以观察这些瓶颈随着时间的推移而发生的变化。该方法是我在日本丰田中央研发实验室工作期间开发的。请看下面关于瓶颈问题的系列文章的完整列表 。
基础知识
正如上一篇文章所讨论的,一个工序在没有被等待打断的情况下,处于活跃状态的时间越长,它就越可能是瓶颈。一个经常因等待物料或等待运输而中断的工序(待机或阻断)不太可能是瓶颈。在上一篇文章中,我们测量了一个工序不被等待打断的平均时间(活跃期)。在这个意义上,活跃意味着不等待(即任何不间断的工作、维修、故障、换型等)。
在这篇文章中,我们现在看一下在任何特定时间段内的最长活跃期。在该时间段内具有最长活跃期的工序就是瓶颈。
分析
假设你有一个有四个工序的系统。对于这四个工序,你会测量工序的活跃时间(工作、故障、维修、定期维护、换型等),以及非活跃时间(等待物料、等待运输)。如果你现在把这些测量值随时间绘制出来,可能会像下图一样。黑色横线代表活跃期,短竖线之间为非活跃期。 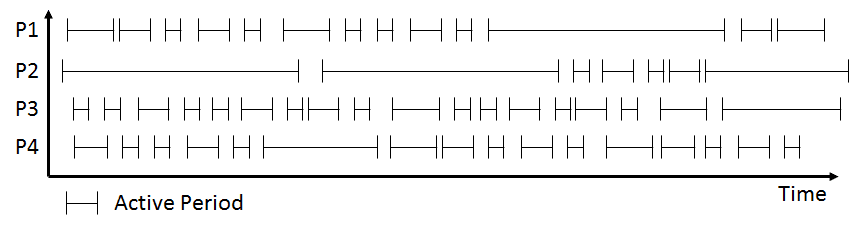 你会看到,在所有情况下,这些线的长度都不是均匀分布的。活跃期法的两个基本原理是:
你会看到,在所有情况下,这些线的长度都不是均匀分布的。活跃期法的两个基本原理是:
- 在任何时候,具有最长的不间断活跃期的工序是瓶颈。
- 在最长的不间断活跃期结束时的重叠期间,瓶颈从一个工序转移到另一个工序。
应用这些原理将得到一个瓶颈表现行为,如下图所示。 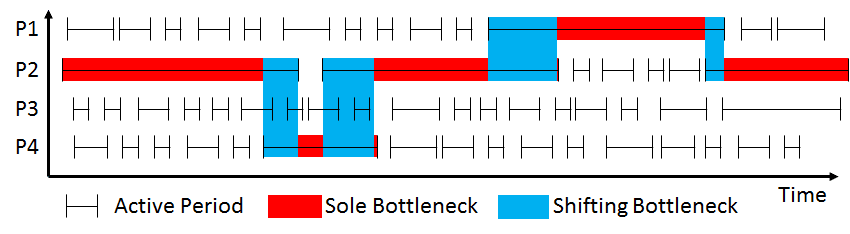 这里,最长的不间断活跃期被标为红色。在这些时间里,相应的工序是系统中唯一的瓶颈。但即使是唯一的瓶颈最终也会被另一个工序打断,因此不再是瓶颈。这时,另一个工序将拥有最长的活跃期,成为新的瓶颈。在两个活跃期重叠期间,瓶颈将从一个工序转移到另一个工序。在上图中,这一段时间以蓝色标记。
这里,最长的不间断活跃期被标为红色。在这些时间里,相应的工序是系统中唯一的瓶颈。但即使是唯一的瓶颈最终也会被另一个工序打断,因此不再是瓶颈。这时,另一个工序将拥有最长的活跃期,成为新的瓶颈。在两个活跃期重叠期间,瓶颈将从一个工序转移到另一个工序。在上图中,这一段时间以蓝色标记。
因此,这种方法可以让你观察到瓶颈随时间的转移。在上面的例子中,最初工序P2是瓶颈。然后瓶颈转移到P4,再转移回P2。之后P1是瓶颈,然后P2再次成为瓶颈。工序P3从未成为瓶颈。
数据总结
根据这一分析,可以看出瓶颈是如何随时间变化的。此外,还可以计算出每个工序成为唯一或变化中的瓶颈的可能性。下面的总结分析显示,工序P2最常成为瓶颈,55%的时间是唯一瓶颈,另外20%的时间是转移瓶颈。如果你想改善你的系统,应该改善工序P2。 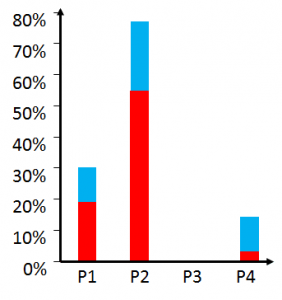 然而,P1在几乎20%的时间里也是唯一的瓶颈,另外10%是转移瓶颈。虽然比P2少得多,但也重要。如果有简单的方法来改善P1,可能对系统也有好处。P4几乎从来不是瓶颈,P3也绝对不是瓶颈,对整个系统性能没有影响。因此,该方法给你一个每个工序成为瓶颈的可能性的精确数据。
然而,P1在几乎20%的时间里也是唯一的瓶颈,另外10%是转移瓶颈。虽然比P2少得多,但也重要。如果有简单的方法来改善P1,可能对系统也有好处。P4几乎从来不是瓶颈,P3也绝对不是瓶颈,对整个系统性能没有影响。因此,该方法给你一个每个工序成为瓶颈的可能性的精确数据。
预测
知道了这些瓶颈的概率,甚至可以根据瓶颈的改进来估计整个系统的改进。唯一瓶颈(Sole Bottleneck,红)的百分比,以及唯一瓶颈加上转移瓶颈(Sole Bottleneck + Shifting bottleneck, 红+蓝)的百分比,是瓶颈的改进对于改进整个系统贡献比例的下限和上限。例如,如果一个工序在80%的时间里是瓶颈,那么瓶颈的节拍时间每改善1秒,就会帮助整个系统的零件间隔平均时间改善0.8秒。
在下图中,我们分析了一个系统的瓶颈问题。对于主要瓶颈的改善,系统的改善被预测为在虚线范围内。真正的系统改进就在这些线之间,直到最后被分析的工序不再是主要瓶颈。  虽然这种预测在实际应用中可能并不需要,但它确实证明了瓶颈识别方法的准确性。
虽然这种预测在实际应用中可能并不需要,但它确实证明了瓶颈识别方法的准确性。
本方法的要求
该方法对所有类型的系统都很有效,包括异序作业、并行系统等。它已经成功地测试了有几十个工序的复杂系统。只要系统是连接的(即不是两个独立的系统),该方法就能发挥作用。
缺点是,它对数据要求非常高。你需要准确地知道每个工序什么时候处于活跃状态或不活跃状态。在大多数情况下,这种数据是很难获得的。如果你有所有需要的数据进行模拟,它确实非常有效,对于通过计算机收集数据的高度自动化系统来说,它也确实有效。
如果没有数据,或者系统的自动化程度较低,那么我强烈推荐“瓶颈漫步–实用瓶颈识别方法第1讲”,在我的下一篇文章中介绍。 这是迄今为止我在实践中首选的方法。
本系列中关于瓶颈的其他文章
- 关于转移瓶颈
- 常见的瓶颈识别方法并不奏效!
- 数学方法精确识别瓶颈1–平均活跃期法
- 数学方法精确识别瓶颈2–活跃期法–如果有大量的数据(如来自模拟的数据)的首选方法
- 瓶颈漫步–实用瓶颈识别方法第1讲–车间内使用的首选方法
- 瓶颈漫步–实用瓶颈识别方法第2讲
参考资料
- Roser, Christoph, Masaru Nakano, and Minoru Tanaka. “Detecting Shifting Bottlenecks.” In International Symposium on Scheduling, 59–62. Hamamatsu, Japan, 2002.
- Roser, Christoph, Masaru Nakano, and Minoru Tanaka. Detection and Monitoring of Shifting Bottlenecks, 2001.
- Roser, Christoph, Masaru Nakano, and Minoru Tanaka. “Monitoring Bottlenecks in Dynamic Discrete Event Systems.” In European Simulation Multiconference. Magdeburg, Germany, 2004.
- Roser, Christoph, Masaru Nakano, and Minoru Tanaka. “Shifting Bottleneck Detection.” In Winter Simulation Conference, edited by Enver Yucesan, C. -H Chen, J. L Snowdon, and John M Charnes, 1079–1086. San Diego, CA, USA, 2002.
- Roser, Christoph, Masaru Nakano, and Minoru Tanaka. “Throughput Sensitivity Analysis Using a Single Simulation.” In Winter Simulation Conference, edited by Enver Yucesan, C. -H Chen, J. L Snowdon, and John M Charnes, 1087–1094. San Diego, CA, USA, 2002.
- Roser, Christoph, Masaru Nakano, and Minoru Tanaka. “Time Shifting Bottlenecks in Manufacturing.” In International Conference on Advanced Mechatronics. Asahikawa, Hokkaido, Japan, 2004.
- Roser, Christoph, Masaru Nakano, and Minoru Tanaka. “Tracking Shifting Bottlenecks.” In Japan-USA Symposium on Flexible Automation, 745–750. Hiroshima, Japan, 2002.
- Roser, Christoph, Masaru Nakano, and Minoru Tanaka. “Utilization Vs. Throughput: Bottleneck Detection in AGV Systems.” InProceedings of the Logistic System Symposium, 67–70. Nagoya, 2002.
Translated by Xie Xuan
