为了提高系统产能，必须找到并改善瓶颈。但寻找瓶颈是很困难的。工业界使用的大多数方法都无法找到瓶颈。正如我在上一篇关于转移瓶颈的文章中所讨论的，这主要是由于瓶颈是动态的，经常从一个工序转移到另一个工序。在这篇文章中，我们将探讨工业界常用的瓶颈识别方法。更重要的是，我们将发现工业界常用的瓶颈识别方法并不奏效。随后的文章将介绍真正有效的瓶颈识别方法。
转移瓶颈参考系统
为了证明几乎所有常用的瓶颈识别方法不奏效，我将使用一个简单的系统作为例子和参考系统。该系统只有三个工序（P1、P2和P3）和四个空间有限的缓冲区域。为了便于理解，该系统将是一个静态系统（见转移瓶颈）–除了静态节拍时间在观察过程中发生变化。缓冲区域假设为足够小，以便在观察的两个阶段中可以迅速消耗或补充。
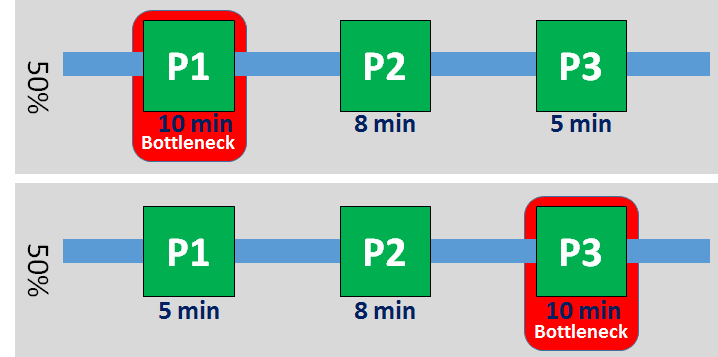
该系统可视化如下。在前一半时间里，工序P1是明显的瓶颈，每个零件的节拍时间为10分钟。在系统运行了一半时间后，节拍时间发生了变化。P1工序的节拍时间降低到5分钟，而P3工序的节拍时间从5分钟增加到10分钟。因此，瓶颈从工序P1转移到工序P3。
我们对瓶颈的定义如下：
在任何时候，系统的瓶颈是制约此时系统产能的工序。
在前一半的时间里，只有当P1的节拍时间发生变化时，系统产能才会发生变化。因此，在前一半的时间里，瓶颈在工序P1。同样地，在后半段时间里，瓶颈是在工序P3。请注意：工序P2永远不会是瓶颈！
至于系统行为变化的原因–这其实并不重要。在现实中，可能是生产的产品发生了变化，软件中的错误，操作人员的失误，或者机器中的一个小缺陷改变了瓶颈的行为。在现实中，你可能有更大的缓冲区域，虽然效果通常不会像上面的例子那样剧烈，但真正的生产系统经常有转移的瓶颈，产生和参考系统一样的效果。 另外，请记住，选择上面的例子是为了便于理解。
出于实际考虑，我们进一步假设系统运行的总时间足够长，与观察时间相比，瓶颈从P1到P3的转变几乎是瞬时的。利用上面这个例子系统，我们现在将测试工业界最常用的瓶颈识别方法。
平均节拍时间
在工业领域，用于寻找瓶颈的最流行的方法可能是看节拍时间。其方法是，节拍时间最长的工序是瓶颈。不巧的是，这对转移瓶颈或改变节拍时间不起作用。
让我们看一下下面的参考系统。在观察期内，工序P1前一半时间的节拍时间为10分钟，后一半时间的节拍时间是5分钟，因此平均节拍时间为7.5分钟。同样地，工序P3的平均节拍时间也是7.5分钟。工序P2从未改变，其平均节拍时间为8分钟。根据使用平均节拍时间的瓶颈识别方法，工序P2一定是瓶颈–只是在现实中它从来都不是。平均节拍时间法在流程中找到的工序从未成为过瓶颈！
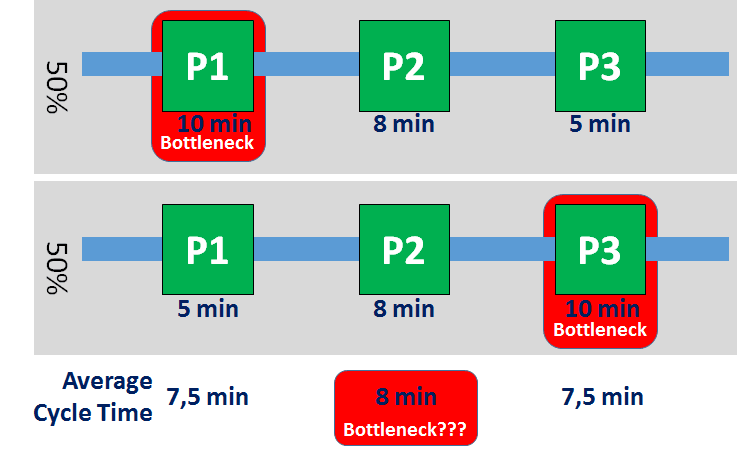
好吧，你可以争辩说，你应该对不同的系统再试一次平均节拍时间方法。但请记住，上面的系统是为了使瓶颈行为容易理解而建立的。在现实中，两个子系统之间不会有如此鲜明的区别，而是一个不断变化的真实系统。尽管如此，平均节拍时间方法的缺陷对真实系统仍然适用。综上所述，使用平均节拍时间识别瓶颈不奏效！
OEE或利用率
使用节拍时间的方法的一个变种是使用总体设备效率（OEE）或设备利用率（关于OEE的细节，请参见我关于测量和操控OEE的系列文章）。这里，利用率或OEE被用来寻找瓶颈。观点是，具有最高OEE或利用率的工序就是瓶颈。
同样，让我们看看下面的参考系统。在一半的时间里，工序P1的OEE为100%，P3为50%。在后半段观察时间内，这些OEE会发生变化。工序P2的OEE始终为80%，这是一个常数。由于每10分钟就有一个零件离开系统，受到瓶颈的限制，工序P2必须等待2分钟，10分钟中工作8分钟。因此，工序P2的OEE为80%。
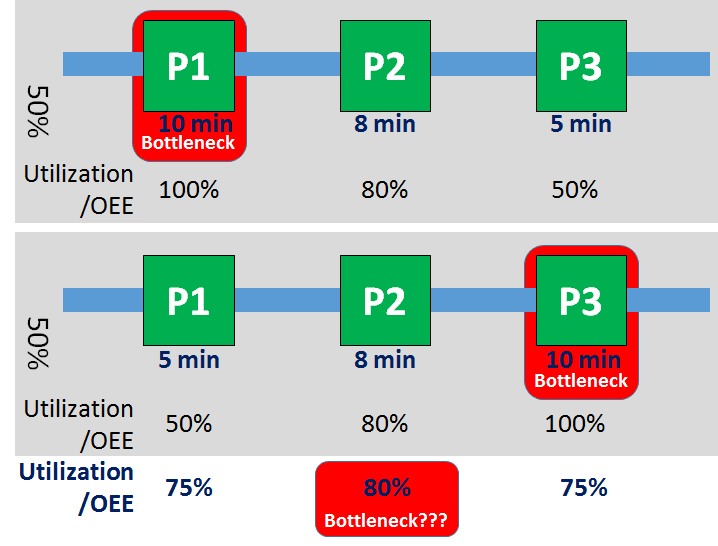
现在我们对两个子系统的OEE进行平均。工序P1和P3的平均OEE都是75%，而工序P2的OEE为80%。因此，根据该方法工序P2一定是瓶颈–但它在现实中从未是瓶颈。OEE方法或利用率方法在流程中找到的工序从未成为过瓶颈！
作为参考，使用OEE进行瓶颈识别可以稍作修改，在OEE中包括额外的损失，包括速度损失、质量损失和可用性损失（参见什么是OEE？）只有零件等待时间或运输时间（缺料或阻断）不应包括在这个修改后的OEE方法中。尽管如此，结果还是一样的，这种改变只是对一个有根本性缺陷的方法进行了微调。综上所述，使用OEE或利用率识别瓶颈不奏效！
平均库存水平
另一种常用的瓶颈检测方法是通过库存水平。其想法是，一个满的缓冲区域表明，瓶颈在缓冲区的下游。而一个空的缓冲区域表明，瓶颈在缓冲区的上游。只要不使用平均数，这种方法就有效。事实上，这是我自己的“瓶颈漫步”方法的两个基石之一。但是一旦我们开始使用平均数，这个方法就会失效。
让我们再看一下我们的参考系统。在前半段观察时间内，工序P1是瓶颈。之前的所有缓冲区域都是满的，之后的所有缓冲区域都是空的（我们在这里把偶尔通过的零件简化为仍然是空的）。同样地，在后半段观察期内，工序P3是瓶颈。之前的所有缓冲区域都是满的，之后的所有缓冲区域都是空的。同样出于简化的原因，我们假设瓶颈从P1到P3的转变与整个时间段相比相当快。
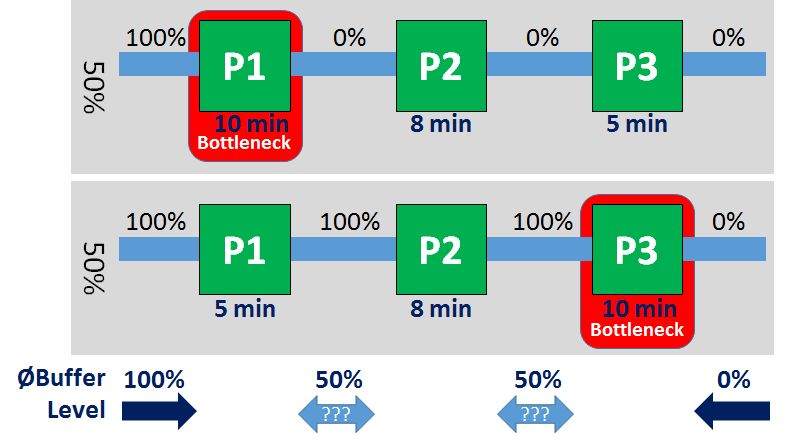
取平均值，我们会发现，工序P1前的缓冲区域总是满的，说明瓶颈在下游。工序P3后的缓冲区域总是空的，说明瓶颈在上游。到目前为止还不错。然而，中间的两个缓冲区域都是50%的库存水平，没有提供任何关于瓶颈的线索。因此，使用平均库存水平的方法并不能找到瓶颈！
在现实中，可能会有更多的随机事件，而平均水平正好是50%的情况很少。然而，根据49%或51%的库存水平来决定瓶颈在哪个方向，在我看来是风险相当大。此外，无论该方法选择哪个方向，它都会遗漏系统中两个瓶颈中任何的一个。综上所述，使用平均库存水平识别瓶颈不奏效！
阻断或待机的平均百分比
最后，我们通过工序被阻断和待机的百分比来识别瓶颈。当一个工序不能将其完成的零件交到下一个缓冲区或工序时，该工序就被阻断了。当一个工序在等待新的零件到来时，该工序就会待机。观点是，一个被阻断的工序表明，瓶颈在该工序下游。一个待机的工序表明，瓶颈在该工序上游。正如库存，这种方法确实有效，是我自己的”瓶颈漫步”方法的第二个基石。但是一旦你开始使用平均数，这个方法就会失效。
让我们再看一下我们的参考系统。在观察上半场，工序P1既没有待机，也没有阻断，而工序P2和P3分别有20%和50%的待机时间（即在10分钟中等待2分钟和5分钟）。同样，在观察下半场，工序P1和P2分别有50%和20%的阻断。同样，出于简化的原因，我们假设瓶颈从P1到P3的转变与整个时间段相比是相当快的。
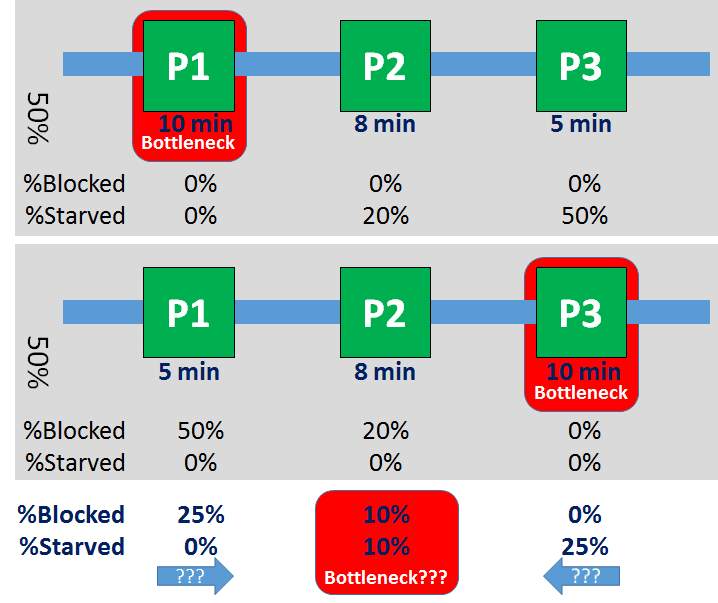
平均而言，工序P1被阻断25%，待机0%，表明瓶颈在P1下游。同样，工序P3被阻断0%，待机25%，表明瓶颈在上游。工序P2阻断和待机都是10%。由于工序P1和P3都指向工序P2，而且工序P2待机和阻断的百分比最低，该方法可以认为工序P2是瓶颈–实际上工序P2从来都不是瓶颈。因此，使用阻断和待机百分比的方法并不能找到瓶颈。
同样，在现实中，结果会不太清楚。然而，即使该方法偶然没有找到工序P2，而是其他工序，它仍然会错过一半的转移瓶颈。这也适用于使用阻断和待机平均百分比的更高级的科学方法，如Kuo等人1996年的文章 (Kuo, Chih-Tsung, J. -T. Lim, and Semyon M. Meerkov. “Bottlenecks in Serial Production Lines: A System-Theoretic Approach.” Mathematical Problems in Engineering 2 (1996): 233–276.)。综上所述，使用阻断和待机平均百分比识别瓶颈不奏效！
结语
如上所述，工业界中几乎所有用于寻找瓶颈的方法在现实中都不起作用。正如丰田很久以前发现的那样。
"永远不要用平均数来识别瓶颈！"
任何使用平均数的瓶颈识别方法都会因为瓶颈的转移而乱了阵脚。由于工业界大多数人都使用平均数的方法，所以大多数人都会对瓶颈是被有自己的看法，但他们大多是错误的。作为我在工业界开展的瓶颈识别工作的一部分，我通常会事先询问工厂的人他们认为瓶颈在哪。人们通常很确定他们知道瓶颈（包括管理层和白领及蓝领工人），但详细的分析证明他们中的大多数人都错了。有50%到75%的人选择了错误的工序作为瓶颈。
更糟糕的是，由于他们没有可靠地确定瓶颈，他们改进了一个对整个系统产能影响不大或没有影响的工序。他们为改善非瓶颈而投入的时间、精力和金钱，不会对整个系统产生任何改善，总之，完全是在浪费精力。
在我随后的文章中，我将展示不同的方法，以可靠地找到瓶颈，即使是转移瓶颈。最重要的是，我最喜欢的方法–“瓶颈漫步“–甚至不需要任何时间测量或数学计算，而只是依靠简单的观察和简单的图形分析。
本系列中关于瓶颈的其他文章
- 关于转移瓶颈
- 常见的瓶颈识别方法并不奏效!
- 数学方法精确识别瓶颈1–平均活跃期法
- 数学方法精确识别瓶颈2–活跃期法–如果有大量的数据（如来自模拟的数据）的首选方法
- 瓶颈漫步–实用瓶颈识别方法第1讲–车间内使用的首选方法
- 瓶颈漫步–实用瓶颈识别方法第2讲
另见
如果你需要学术引用，请引用以下文献：
Roser, Christoph, and Masaru Nakano. “A Quantitative Comparison of Bottleneck Detection Methods in Manufacturing Systems with Particular Consideration for Shifting Bottlenecks.” In Proceedings of the International Conference on the Advances in Production Management System. Tokyo, Japan, 2015.
Translated by Xie Xuan