 After all the theory on how a milk run works, it is finally time to calculate the quantitative details of the milk run. Since this takes a bit longer, I have split the calculations into two separate posts. Well, here we go!
After all the theory on how a milk run works, it is finally time to calculate the quantitative details of the milk run. Since this takes a bit longer, I have split the calculations into two separate posts. Well, here we go!
Frequency and Capacity
 There are a few things on a milk run that influence or depend on each other. The capacity of the train, the frequency of the train, the number of materials supplied, and the space at the assembly line. In theory, a cost-benefit analysis would guide you toward the optimal solution. Unfortunately, in real life you do not have the costs and the values associated with these effects, and I believe a reasonable cost-benefit is not possible.
There are a few things on a milk run that influence or depend on each other. The capacity of the train, the frequency of the train, the number of materials supplied, and the space at the assembly line. In theory, a cost-benefit analysis would guide you toward the optimal solution. Unfortunately, in real life you do not have the costs and the values associated with these effects, and I believe a reasonable cost-benefit is not possible.
Instead, I would suggest starting at one end and working your way toward the dependent variables. Out of all these factors, the space at the assembly line is the most critical one. Hence, your milk run should be set up to minimize the use of this space. You probably have to repeat the calculations below a few times iteratively to come to a suitable solution.
You Need Two Cycles’ Worth of Material Plus One Box in the Loop
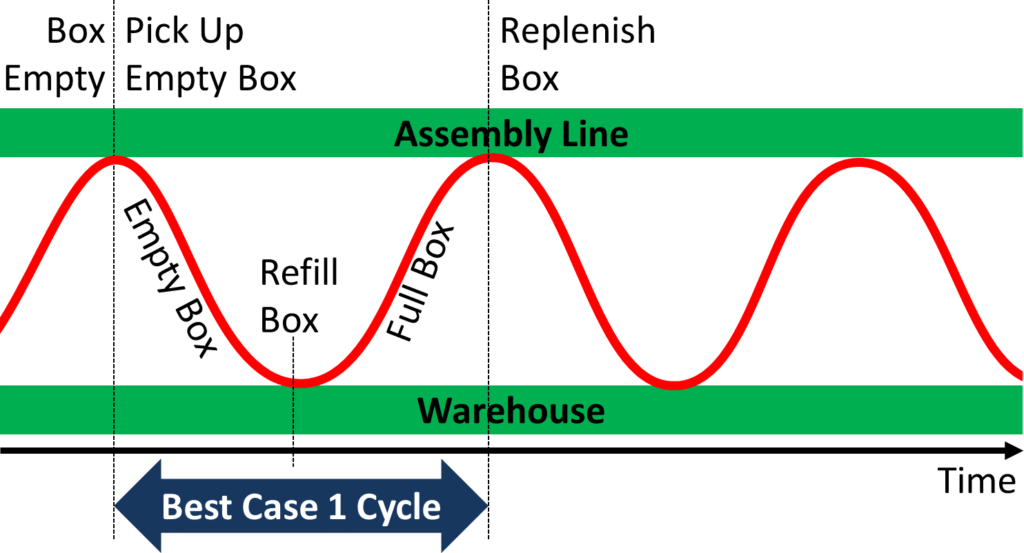
So let’s start with the space at the assembly line. We want to figure out how much material we need at the line. You always want to have at least one box of material there all the time. Let’s look at one box in more detail. If you have just emptied the box, the milk run would pick it up on its next visit, and bring it back full on the second visit after that. In the best case, your box would be empty just when the milk run arrives, and you would have to wait one milk run cycle to get a new box (i.e., if the milk run comes every hour, you would get a full box back in one hour). This is illustrated below on a timeline where the red line represents the milk run traveling from the warehouse to the assembly line stop and back.
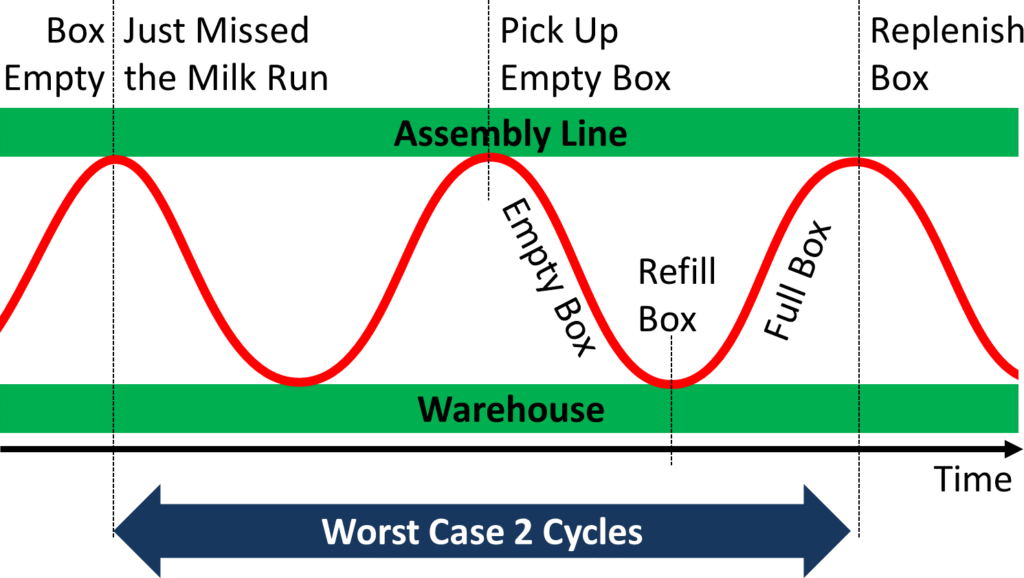
In the worst case, however, your box becomes empty just when the milk run left, and you would have to wait a maximum of two cycles. If the milk run visits every hour, you would have to wait one hour for the milk run to pick up the empty box, and another hour to bring you the box back full. Hence the total replenishment time is two milk run cycles, or in our example two hours. This is also illustrated below.
Both the best case and the worst case are possible. Hence, we have to set up the milk run to handle the worst-case scenario. Since this worst case won’t happen all the time, this assumption also gives us some safety buffer for the “not-the-worst” cases. Therefore we need enough space at the line to store material worth for two cycles duration plus one box! We need this extra box of material in case all other boxes are empty or refilled and just on the way back from the warehouse. You can add some additional safety buffer if you feel uncomfortable with the number.
In regular operation, half of the inventory (plus safety buffer) would be at the assembly line, whereas the other half would be on the milk run (either empty to the warehouse or full returning from the warehouse). You may get away for regular operations with space at the assembly line for material for only one cycle (plus safety), while the material for the other cycle (plus safety) is on the milk run. However, in this case material may back up in the milk run if the demand is unusually low.
In any case, when the milk run is operating, check the status of the supermarket at the line. If there are occasional stock-outs despite material in the warehouse, you may want to increase the number of boxes. If there is always more than one box in the supermarket, you may want to reduce the number of boxes.
Estimate the Milk-Run Cycle Time
Next, we would need to make an initial estimate on what our milk-run cycle can be. This, of course, will be revised later iteratively to find a good solution.
So how often does your milk run run? Do you have one every two hours, one every hour, one every thirty minutes, or even one every fifteen minutes? The shorter the cycle, the less material you need at the assembly line. However, the shorter the cycle the more milk runs you may need.
You may have noticed above that I used nice, round numbers for the duration. You could of course determine that you want a milk run every twenty-three minutes and fifteen seconds. This would work, but it would drive your people crazy. Your driver would have to check every time when his next round is due. However, if your cycle is somewhat regular (hour-sided intervals, or an even division of the hour (thirty minutes, twenty minutes, fifteen minutes or so), the driver and also the customer can remember it much easier and will notice much faster if something is out of whack. For an automated transport system, you could in theory also use odd numbers, but even then the customer may wonder when his next vehicle would arrive.
How Much Is Two Cycles Plus One Box?
Okay, let’s figure out how much material you need to cover two cycle times plus one box. Determine what material types you need at the assembly line, what their consumption rate (or consumption takt) is, and how many of them you want to put in a box. For example, assume you need on average one piece of type A every 50 seconds (the consumption takt). If your box fits 12 pieces, then one box will be enough for 10 minutes of consumption (12 times 50 seconds equals 600 seconds or 10 minutes).
Hence, if your cycle is (for example) 1 hour, then you would need 6 boxes to cover the one hour, plus one (i.e., a total of 7 boxes of this particular material type).
In this example I had nice round numbers. Chances are that you may end up with a non-integer number of boxes (i.e., 7.3 boxes to cover the two cycle). In this case, always round up! Strictly speaking you may not need the additional +1 box in this case, but whenever possible I prefer to add this +1 anyway to be on the safe side.
Hence, the calculation of the total number of boxes in the loop is as follows:
\[ { No. \: of \: Boxes = Round \: Up (\frac{( 2 \cdot Milk \: Run \: Cycle \: Time)}{Consumption \: Takt \cdot Pieces \: per \: Box}) +1 } \]where the consumption takt is as follows:
\[{ Consumption \: Takt = \frac{ Time \: Interval}{Demand \: during \: Time \: Interval} } \]This calculation has to be repeated for every material that you want to provide by milk run. The consumption rate may change depending on the part (i.e., one product may require four screws and one flange per piece, hence the hourly demand or the time between pieces may differ). The number of parts in a box or container may also differ depending on the part number. But overall you now have the number of boxes that you need to fit at the milk-run stop supermarket. This has to be done at every station for all the material that goes on the milk run.
In the next post I will continue these calculations with discussion of the milk run layout. Until then stay tuned, and go out and organize your industry!

The main objective here should be to create a Pull from the say assembly line. Hence Takt, each bin qty and bins per truck load of the milk run vehicle! Then decide how to optimise the time taken for each trip. Yes as you have rightly said, you shouldn’t flood parts during milk run, no matter the milking vehicle is not really full !
Very nice. I assume stop times and travel times in relation to the overall milk run time will be covered in the next one. Look forward to it.
Thanks Chris ,for my understanding for space at assembly is 1 cycle plus safe buffers not the all space including 2 Cycles Plus One Box,is it right?
Hi Felix, if everything works fine you would need only space for 1 cycle plus one box at the line. However, if there are some delays, more material will arrive. It is often easier to provide the extra space rather than to have the milk run bring the material back and try again on the next run.
How would the calculations change, assuming that the assembly line sends a signal of “empty box” to the warehouse, instead of waiting for the milk run to come?
Hi Juan, very good point. I have this calculation as an example for the external milk run in an upcoming post. With external milk runs the “empty” signal is often digital and much faster. Within the plant it is often easier to simply bring the box back rather than a digital system.
Hello,
I have a question about figure 1. There the milkrun only takes away the empty box, refils it at the warehouse and returns the full box.
Is there also a version of a milk run, where the empty boxes are taken away and being replaced with full boxes at the same time? Like in the example of the original milk run in the post “introductions to Milk Runs”.
Hello Andreas, The question is: How does the milk run know what to bring. The empty box is the signal for replenishment, and the milk run gets the signal only when he picks up the empty box.
There are ways around that using digital technology, e.g. scanning the box when empty, but this makes it a lot more difficult to set up, and may have other potential ways to fail.